常见排序算法-堆排序

前几天去某家公司面试，被要求手写和推导堆排序算法（比如建堆的时间复杂度为什么是O(n)），其实大二学了这个之后基本就没怎么看了，所以导致当是面试的情景很是尴尬。但堆排序其实是一个极其常见基础算法，写不出来真的不能怪面试官，还是自己基础不够扎实。那么下面就再来复习一下堆排序得原理。

二叉树

要了解堆首先需要了解一下二叉树，在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树（BST）和二叉堆。

满二叉树：一棵深度为 k，且有 2^k - 1 个节点称之为满二叉树。

下图是一棵深度为4的满二叉树。

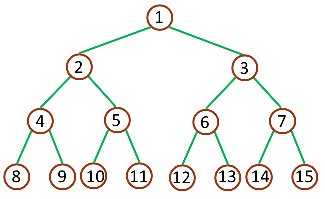
完全二叉树：深度为 k，有 n 个节点的二叉树，当且仅当其每一个节点都与深度为 k 的满二叉树中序号为 1 至 n 的节点对应时，称之为完全二叉树。即前k-1层为满二叉树，第k层的结点都在该层的最左边。

下图是一棵深度为4的完全二叉树。

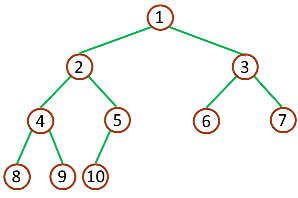
堆

堆（二叉堆）可以视为一棵完全的二叉树。完全二叉树的一个“优秀”的性质是，除了最底层之外，其余每一层都是满的，这使得堆可以利用数组来表示（普通的一般的二叉树通常用链表作为基本容器表示），每一个结点对应数组中的一个元素。

如下图，是一个堆和数组的相互关系。

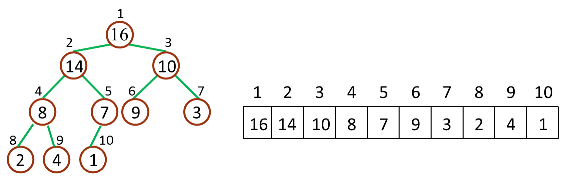
对于给定的某个节点的下标i，可以很容易的计算出这个结点的父结点、孩子结点的下标：

Parent(i) = i/2 // i 的父节点下标
Left(i) = 2i // i 的左子节点下标
Right(i) = 2i + 1 // i 的右子节点下标

然后，堆（二叉堆）又分为2种：最大堆（大顶堆）、最小堆（小顶堆）。

最大堆

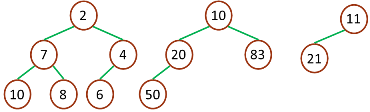
堆中的最大元素值出现在根结点（堆顶）
堆中每个父节点的元素值都大于等于其孩子结点（如果存在）

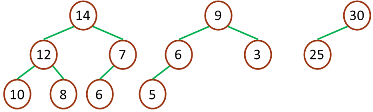
最小堆

堆中的最小元素值出现在根结点（堆顶）
堆中每个父节点的元素值都小于等于其孩子结点（如果存在）

堆排序

堆排序就是把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作：

堆调整
建堆

继续进行下面的讨论前，需要注意的一个问题是：数组都是 Zero-Based，这就意味着我们的堆数据结构模型要发生改变：

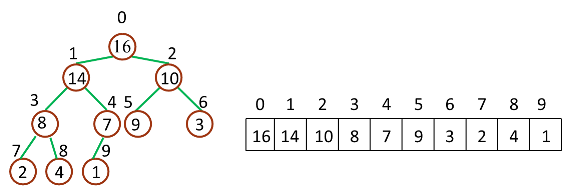
相应的，几个计算公式也要作出相应调整：

Parent(i) = (i-1)/2 // i 的父节点下标
Left(i) = 2i + 1 // i 的左子节点下标
Right(i) = 2i + 2 // i 的右子节点下标

堆调整

最大堆调整（Max‐Heapify）的作用是保持最大堆的性质，是创建最大堆的核心子程序，作用过程如图所示：

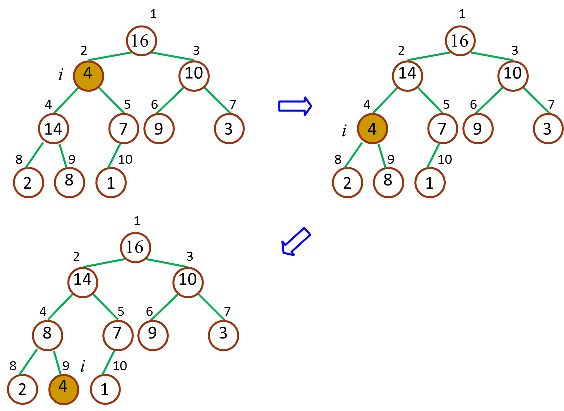
由于一次调整后，堆仍然违反堆性质，所以需要递归的测试，使得整个堆都满足堆性质，用 Java 可以表示如下：


/**
 * 最大堆调整
 * @param array
 * @param index 检查起始的下标
 * @param heapSize 堆大小
 */
public void heapify(int[] array, int index, int heapSize) {
    int left = 2 * index + 1;// 左孩子的下标（如果存在的话）
    int right = 2 * index + 2;// 左孩子的下标（如果存在的话）
    int iMax = index;// 寻找3个节点中最大值节点的下标

    if (left < heapSize && array[left] > array[index])
        iMax = left;
    if (right < heapSize && array[right] > array[iMax])
        iMax = right;

    if (iMax != index) {
        swap(array, iMax, index);
        heapify(array, iMax, heapSize);
    }
}

public void swap(int[] array, int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

递归在调用递归子函数的时候，会先将传给子函数的参数压栈，然后将当前指令的下一条指令的地址压栈，以便子函数执行完后返回到原函数中继续执行，在原函数继续执行之前还涉及到清理子函数的栈。因此，递归的效率比迭代低一点点。其实上面的调整堆也可以用迭代来实现：

public void heapify(int[] array, int index, int heapSize) {
    int left, right, iMax;
    while (true) {
        left = 2 * index + 1;// 左孩子的下标（如果存在的话）
        right = 2 * index + 2;// 左孩子的下标（如果存在的话）
        iMax = index;// 寻找3个节点中最大值节点的下标

        if (left < heapSize && array[left] > array[index])
            iMax = left;
        if (right < heapSize && array[right] > array[iMax])
            iMax = right;

        if (iMax != index) {
            swap(array, iMax, index);
            index = iMax;
        } else
            break;
    }
}

建堆

创建最大堆（Build-Max-Heap）的作用是将一个数组改造成一个最大堆，接受数组和堆大小两个参数，Build-Max-Heap 将自下而上的调用 Max-Heapify 来改造数组，建立最大堆。因为 Max-Heapify 能够保证下标 i 的结点之后结点都满足最大堆的性质，所以自下而上的调用 Max-Heapify 能够在改造过程中保持这一性质。如果最大堆的数量元素是 n，那么 Build-Max-Heap 从 Parent(n) 开始，往上依次调用 Max-Heapify。流程如下：

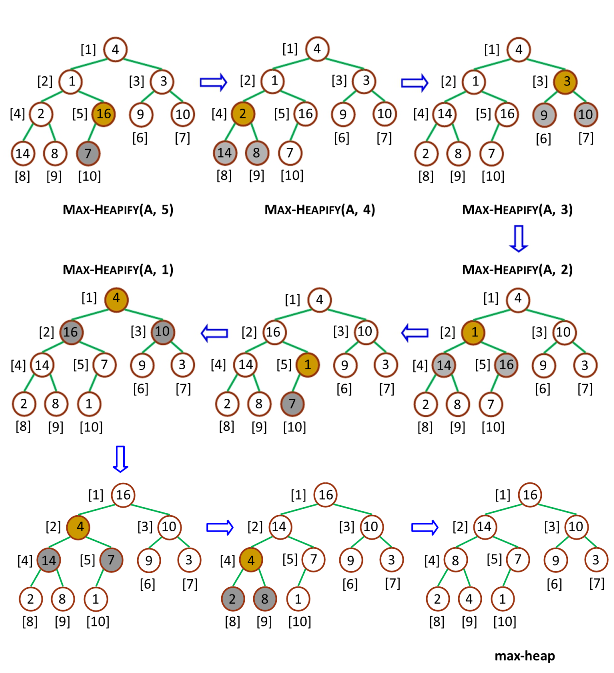
用 Java 描述如下：

public void buildHeap(int[] array) {
    int n = array.length;// 数组中元素的个数
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(array, i, n);
}

堆排序

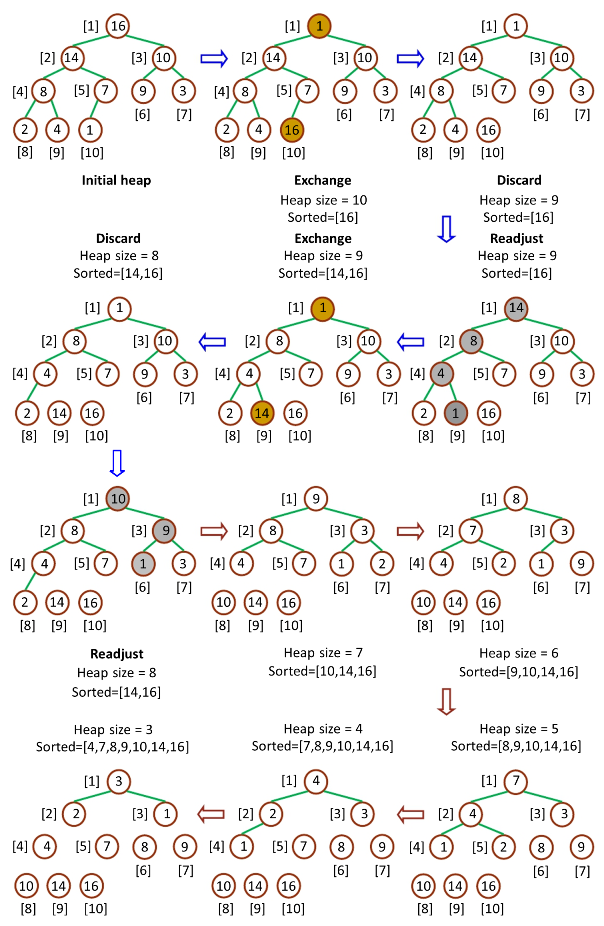
堆排序（Heap-Sort）先调用Build-Max-Heap将原数组改造为最大堆，这个时候堆定元素最大，将其与堆底（当前堆对应数组的最后一个元素）交换，堆的大小减去1，当前堆堆底后面的元素已经排好序。然后，从堆顶元素开始检查，调用Max-Heapify保持最大堆性质，这样可以将第二大的元素调到堆顶，然后将其与当前堆堆底元素交换。重复这个过程n-1次，直到堆中只有1个元素为止。整个流程如下：

public class HeapSort {
    public void heapSort(int[] array) {
        buildHeap(array);// 构建堆
        int n = array.length;
        for (int i = n - 1; i >= 1; i--) {
            swap(array, 0, i);
            heapify(array, 0, i);
        }
    }

    // 创建最大堆
    public void buildHeap(int[] array) {
        int n = array.length;// 数组中元素的个数
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(array, i, n);
    }

    /**
     * 最大堆调整
     * 
     * @param array
     * @param index 检查起始的下标
     * @param heapSize 堆大小
     */
    public void heapify(int[] array, int index, int heapSize) {
        int left = 2 * index + 1;// 左孩子的下标（如果存在的话）
        int right = 2 * index + 2;// 左孩子的下标（如果存在的话）
        int iMax = index;// 寻找3个节点中最大值节点的下标

        if (left < heapSize && array[left] > array[index])
            iMax = left;
        if (right < heapSize && array[right] > array[iMax])
            iMax = right;

        if (iMax != index) {
            swap(array, iMax, index);
            heapify(array, iMax, heapSize);
        }
    }

    public void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
}